アクリル仕上げフロントパネル採用ケースを開発致しました。
デザインスケッチと、試作機の写真を掲載します。
ご覧のように、フロントパネルにグロッシーな輝きと透明さを持つアクリルプレートを取り付けるケースを開発致しました。
同時に、全体の構造もスリムに致しました。
特に、フロントパネルの美しさが長期間保たれるケースです。
今後、このケースを採用したアンプを発売予定ですが、アンプ価格は現在とほぼ同一となるように検討しております。

新開発アクリル仕上げフロントパネル採用ケース デザインスケッチ
フルバランスパッシブプリアンプ“MASTERS CA-999FBN/A”


新開発アクリル仕上げフロントパネル採用ケース 試作機実物写真
Xカレント回路採用プリメインアンプ“MASTERS AU-777X CUSTOM”
スルーレート(Slew Rate)とは
スルーレートというと、アンプの立ち上がり応答性を意味すると理解される方がおられますが、これは誤解です。
気になったのは、あるオーディオ誌の記事中で、評論家の方が、“スルーレートの高いアンプはスピード感がある”というような記述をされていたことです。
また、1970年代後半のオーディオアンプ回路開発競争時には、競って、スルーレート値の高いことを誇示していました。そういえば、サンスイのダイアモンド差動回路は入力が大きくなると、電源電圧にまで半導体デバイスがONする性能を有していたので、スルーレートは200V/μsを超える値に結果的になっておりました。
スルーレートはどう測定するかと言うと、【図2】【図3】に示すように、入力に10kHzの矩形波を加え、オシロスコープで、決められた周期(1μVあたり)で、アンプ出力が何Vに立ち上がるかを測定します。
その値は最大出力電圧の最大傾斜(変化率:dV/dt)を示します。
従って、そのアンプにそれ以上の出力電圧を求めても、応答できず、サイン波入力の場合、その形はやせ細り、三角波に変わっていきます。
こう見ると、いかにもアンプの瞬時応答性を示すように思いがちです。
スルーレートはそうではなく、【図1】に示すように、サイン波において、高域で、どの程度電圧を出せるかを示す定常特性です。
もっと、分かりやすく言えば、“高域における出力帯域幅(Power Band Width)の別な表現”とも言えます。それは最大出力電圧において、とりうる周波数の上限を意味します。
そして、サイン波によるアンプ出力電圧とで
の関係にあります。(黒田徹著:トランジスタアンプ設計法より引用)
【写真1】にスルーレート測定画像を示します。
スルーレートから高域パワーバンドへの計算例
例えば、1kHzで30W(15.5V/8Ω)のパワーアンプのスルーレートが2V/μsであったら、
となり、30Wを出せる高域周波数帯域幅は、高域に関しては15kHzで、それ以上にサイン波を入力すると、出力は三角波に変形することを意味しています。
また、スルーレートは、アンプの負荷抵抗の影響は理論的に受けません。
スルーレートから言えること
- 出力の小さいアンプのスルーレートは小さくて良い。出力の大きなアンプはそれなりのスルーレートが必要。
- CHアンプシステムならば、低域,中域用アンプのスルーレートは低くて良い。
スルーレートとアンプ設計との関係
普遍的には、
の関係があります。
具体的に、半導体アンプでは、初段差動回路に流す電流と、初段回路の負荷容量とで決まります。
スルーレートを大きくして、高域最大出力電圧を大きくするには、初段電流を大きくして、位相補償を含む負荷容量を小さくすればよいことが分かります。
負荷容量を小さくすることは、NFBによる発振安定度に関係し、アンプのNFB量、アンプゲインに関係してきます。
一方、真空管アンプでも、初段電流と初段回路の負荷抵抗に並列に付加される位相補償回路で、スルーレートの値は影響を受けます。
スルーレートの一般的な数値とその意味
半導体OPアンプでは、使用する最大電圧が2V以下とか、低い電圧では、スルーレートは1V以下でも問題ない。
高周波領域(10MHz以上とか)に使用するOPアンプで、10Vくらいの出力を必要とするなら、スルーレートが1000V必要なことは分かる。
冒頭に述べたサンスイのダイアモンド回路を採用したAU-D907(100W出力)では、200V/μsでしたから、どの程度の高域周波数が扱えるかを計算してみます。
となり、ものすごい高域周波数能力を持っていることが分かります。
通常の半導体アンプでは10V~60Vくらい。真空管アンプで、3V~10Vくらいが普通です。
ちなみにMASTERS半導体パワーアンプでは40V/μsくらいです。
音質、音調との関連
一概には言えません。
体験的には、低いアンプはしっとりする反面、行き過ぎるともっさり、切れ味鈍いサウンドになりがちです。
そのアンプの最大出力において、その出力電圧波形が三角波になるような現象がなく、1kHzと大差ないひずみ率なら問題ありません。
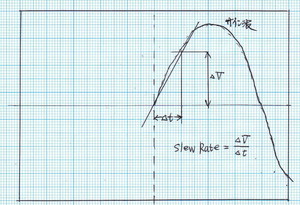
【図1】スルーレートと高域周波数の再生能力との関係
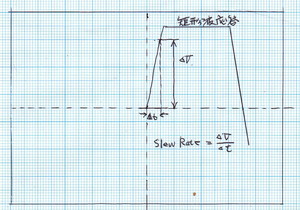
【図2】オシロスコープ画像上での測定,観測法
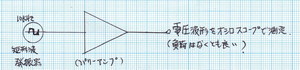
【図3】スルーレート測定ブロックダイアグラム
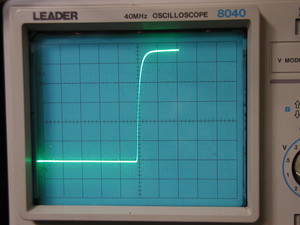
【写真1】スルーレート測定画像
当社が製作しているクロスオーバー周波数可変方式は、他にないユニークで、実際のCH間のサウンドバランス調整に大変役立って、便利で、順調に注文を頂いております。
そのようななか、かねてから知っているFさんから、引き算式チャネルデバイダ(以下、「チャネルデバイダ」を「CHデバイダ」と記載します)を造ってもらえないかというリクエストを頂きました。
いきなり引き算式と言われて、戸惑ったのですが、落ち着いて考えると、20年くらい前、設計会社をやっていた頃、SONYの委託を受けた会社のKGさんから、引き算式の設計依頼を受け、設計、試作したことを思い出しました。
例えば、2CHデバイダを設計する際、普通は、低域側にはローパスフィルタ、高域側にはハイパスフィルタを設けて、構成します。
この方式は、6dB/octフィルタでは、フィルタの位相シフトがクロスオーバーポイントでは45度となり、どの帯域でも、低域と高域の和は一定であり、いわゆる伝達関数は1となります。但し、減衰量が緩いために、低域側と高域側とが相互干渉して、音響バランス上うまくいかないケースが多いのです。
そのような理由で、普通、CHデバイダは12dB/oct以上の減衰量のCHデバイダが主流です。けれども、この方式は、位相シフトがクロスオーバー周波数において、90度になるために、逆相になるため敬遠する方が稀におられます。そのような状況をクロスオーバー周波数を可変とすることで、最適ポイントを見つけ出すのがマスターズのCHデバイダです。
また、このような問題点を一掃する方式として、デジタルCHデバイダがあります。この方式は位相シフトの問題はまったくなく、自由に減衰量を設定できます。例えば、ー90dB/octのような凄い減衰特性も得られます。
事実、デジタルCHデバイダーを採用したCHアンプシステムを、2人の御宅で聴きましたが、サウンドバランスは素晴らしく、自然で好ましく、以前、その感想をブログで報告したことがあります。
けれども、サウンド品位を重視する方から、“A/D,D/Aプロセスを繰り返すので、デジタルCHデバイダは少し問題がある”ということを聞いたことがあります。
そのような状況で、引き算式CHデバイダとは、上記の2CHデバイダの時は、低域側にローパスフィルタを設置し、それを低域出力にすることは変わりませんが、高域側の出力は、入力信号から、低域側の成分を引けば、残りの成分は高域成分になります。これが、引き算式CHデバイダの基本的な考え方です。
詳細は省きますが、この方式で、-12dB/oct方式を採用しようとすると、位相シフト変化により、-6dB/oct方式と同じ結果になり、伝達関数は1になっても、減衰量に上述したような不具合が生じてしまいます。
この欠点を、1960年代の後半に、山中氏が、遅れた位相を進める補正フィルタを増設することによって、-12dB/octの特性を示しつつ、伝達関数1を達成できました。以後、引き算式フィルタによるCHデバイダは、山中(氏)の方式と言うようになりました。
それから、40年以上経た現在、山中式CHデバイダは私の知る限り市販されてないようです。具体的に引き算することは、OPアンプの反転回路を使えば、実現できます。
Fさんのご依頼により作成した、3CHデバイダのブロックダイアグラムを【図1】に示します。
完成まで2か月掛かりましたが、3点クロスオーバー周波数切り換え型のCHデバイダが出来上がりました。
確かに、入力信号とCHデバイダ出力総和とはまったく同じになり、伝達関数1が達成されます。
回路を重視される方は、この結果に狂喜されると思います。
私はスピーカ量産設計の経験から、音響バランスを重視しますので、引き算式が最高とは断言しませんが、ひとつのCHアンプシステムにおける方法と思います。
もし、引き算式CHデバイダを採用してみたい方がおられましたら、是非、ご一報ください。カスタム、一品製作アンプとして、引き受けます。
CHアンプ愛好者の方、ご検討願います。
<2015年7月19日追記>
【写真1】のイメージ画像のCHデバイダができました!!
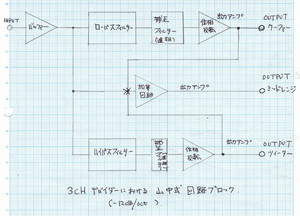
【図1】3CHデバイダにおける中山式回路ブロック(-12dB/oct)

【写真1】チャネルデバイダ“MASTERS CH-303Y/CUSTOM”